Matriz de distancias geodésicas

Alex

Esta semana he tenido unos días tranquilos, sin teléfono, sin mails, sin alumnos… así que además de poner a punto mi ordenador, he aprovechado para programar una función pendiente del proyecto Rutas.

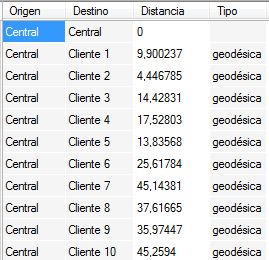
matriz de distancias geodésicas

Se trata de un procedimiento de cálculo rápido de la matriz de distancias mínimas e itinerarios mediante líneas geodésicas. En realidad la distancia calculada no será la real del itinerario entre dos puntos, sino una aproximación mediante un cálculo geogésico (véase ejemplo de google maps).

Este cálculo rápido simplifica y facilita la resolución de algunos problemas de tipo estratégico, donde no es tan importante la precisión de la solución sino la valoración global del problema. Aquí os dejo algo de código fuente por si fuera de vuestra utilidad:

'Constantes para cálculos trigonométricosPublic Const Pi As Double = 3.14159265358979 ' PI=22/7, Pi = Atn(1) * 4
Public Const DtoR As Double = (pi / 180.0#) ' Grados a RadianesPublic Const RtoD As Double = (180.0# / pi) ' Radianes a Grados
Public Function Distancia_km_2puntosTierra(ByVal Lat1 As Double, ByVal Lat2 As Double, ByVal Lon1 As Double, ByVal Lon2 As Double) As Double
        ' Calcula la distancia entre dos puntos de la superficie de la tierra        ' La distancia más corta entre dos puntos de la superficie de la tierra es
        ' d = arccos{cos(Dlat) - [1 - cos(Dlong)]cos(lat1)cos(lat2)}
        ' Dlat = lab - lat2
        ' Dlong = 10ng. - long2
        ' lati, = latitude of point i
        ' longi, = longitude of point i
        ' Factores de conversión, una milla nautica equivale a:
        '   6076.10 feet (pies)
        '   2027 yardas
        '   1.852 km
        '   1.151 statute mile
        ' los cálculos trigonométricos en basic se hacen en Radianes
        ' y no en grados, por eso el dato de entrada se debe dividir por 
        '  57.2958 (que es 180/pi, el número de grados de un radián).
        'Conversión de grados a radianes es:
        'Grad=400-degrees/0.9 or Degrees=0.9x(400-Grad)
        Dim D As Double
        Dim L1 As Double, L2 As Double
        Dim I1 As Double, I2 As Double
        L1 = Lat1 * DtoR
        L2 = Lat2 * DtoR
        I1 = Lon1 * DtoR
        I2 = Lon2 * DtoR
        D = Math.Acos(Math.Cos(L1 - L2) - (1 - Math.Cos(I1 - I2)) * Math.Cos(L1) * Math.Cos(L2))
        Distancia_km_2puntosTierra = D * 60 * RtoD * 1.852 'se multiplica para pasar de NM a km        ' One degree of such an arc on the earth's surface is 60    End Function

Si te interesa este tema, puedes leer más sobre: elipsoide, geodesia, proyección de Mercator.

Por otro lado, me he instalado el nuevo Visual Studio 2008, e importado con éxito todo el código fuente generado hasta la fecha. Parece que el nuevo IDE va bien, pero que muy bien.